선택 정렬이란?
최소값 탐색 후 가장 앞 자리로 옮기며 정렬하는 알고리즘
시간 복잡도
최상 : \( O(n^2) \)
최악 : \( O(n^2) \)
관련 글
[Algorithm] Sort #1 - 버블 정렬 Bubble Sort
[Algorithm] Sort #3 - 삽입 정렬 Insertion Sort
[Algorithm] Sort #4 - 병합 정렬 Merge Sort
[Algorithm] Sort #5 - 힙 정렬 Heap Sort
[Algorithm] Sort #6 - 퀵 정렬 Quick Sort
알고리즘의 기본이라고 할 수 있는 정렬에서 두 번째는 선택 정렬입니다.
알고리즘
선택 정렬의 알고리즘은 다음과 같습니다.
- 리스트에서 최소값 원소를 찾는다.
- 최소값과 첫번째 원소의 위치를 바꾼다. (이미 정렬된 원소는 제외)
- 1,2의 과정을 n-1번 진행한다.
선택 정렬 예시
{ 9, 1, 7, 5, 2} 순서대로 원소가 존재한다고 가정했을 때 선택 정렬의 예시는 다음과 같습니다.
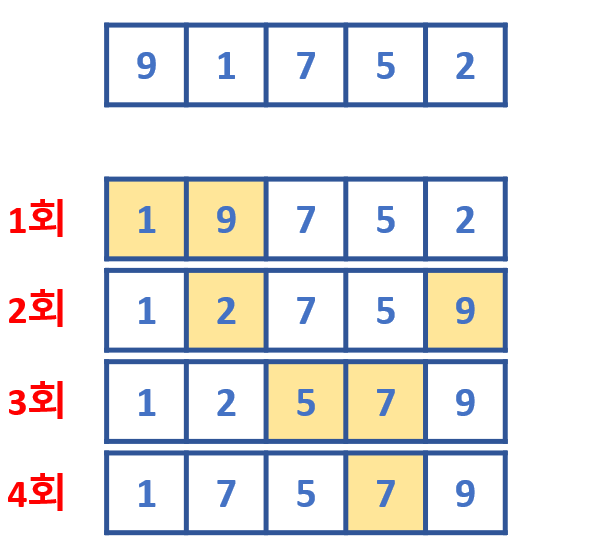
이전 글에서 설명한 버블 정렬에 비해 과정이 단순해보이지만 위 그림에서는 생략된 부분이 있습니다. 생략된 것은 바로 원소 리스트에서 최솟값을 찾는 과정입니다. 위치를 한번 바꿔줄 때마다 남은 원소 중에서 최솟값을 찾는데 필요한 시간을 감안하면 결코 빠른 시간은 아닙니다.
시간 복잡도 계산
선택 정렬의 시간복잡도는 최악, 최상의 경우 모두 동일합니다.
각 정렬 회차에 따라 최솟값을 찾기 위해 n-1, n-2, n-3 ..... 2, 1번 비교하고 정렬을 n-1번 하기 때문에 시간 복잡도는 \( O(n^2) \)입니다.
하지만 시간복잡도가 버블 정렬과 같음에도, 선택 정렬은 버블 정렬보다 항상 우수하다고 말할 수 있습니다. 그 이유는 버블 정렬은 정렬을 1회 할 때마다 최대 n-1번의 swap 과정이 필요하지만 선택 정렬은 1번의 swap만 진행하기 때문입니다.
C++ Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
vector<int> arr = {9,1,7,5,2};
for(int i=0; i<arr.size()-1; i++){
int minP = i;
for(int j=i+1; j<arr.size(); j++)
if(arr[j] < arr[minP])
minP = j;
swap(arr[i], arr[minP]);
}
for(int i=0; i<arr.size(); i++)
cout << arr[i];
}'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Sort #6 - 퀵 정렬 Quick Sort (0) | 2021.01.16 |
|---|---|
| [Algorithm] Sort #5 - 힙 정렬 Heap Sort (0) | 2021.01.09 |
| [Algorithm] Sort #4 - 병합 정렬 Merge Sort (0) | 2021.01.08 |
| [Algorithm] Sort #3 - 삽입 정렬 Insertion Sort (1) | 2021.01.04 |
| [Algorithm] Sort #1 - 버블 정렬 Bubble Sort (0) | 2020.12.29 |
![[Algorithm] Sort #2 - 선택 정렬 Selection Sort](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FxAiAM%2FbtqR3Q7hGTN%2FAAAAAAAAAAAAAAAAAAAAAHPeENbUPW8Bap-0TdBMI9CFDigIzpQIcKY32lzVijh6%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DiBYC5srdR0DiXYyp7%252Bnozms1rds%253D)