퀵 정렬이란?
Pivot을 기준으로 작은 값, 큰 값들로 나눠 정렬하는 알고리즘
시간 복잡도
최상 : \( O(n \log n) \)
최악 : \( O(n^2) \)
관련 글
[Algorithm] Sort #1 - 버블 정렬 Bubble Sort
[Algorithm] Sort #2 - 선택 정렬 Selection Sort
[Algorithm] Sort #3 - 삽입 정렬 Insertion Sort
[Algorithm] Sort #4 - 병합 정렬 Merge Sort
[Algorithm] Sort #5 - 힙 정렬 Heap Sort
평균 시간 복잡도가 \( O(n \log n) \)인 정렬 알고리즘 중 마지막은 퀵 정렬입니다. Pivot을 정한 후 두 그룹으로 나눈다는 것에서 병합 정렬과 비슷하게 보이지만, 퀵 정렬은 Pivot을 기준으로 정렬 후 분할합니다. 정렬되는 과정이 분할 과정에서 이루어지는지 병합 과정에서 이루어지는지가 가장 큰 차이점이라고 할 수 있습니다. 병합 정렬, 힙 정렬과 시간 복잡도는 같지만 퀵 정렬이 평균 속도로는 가장 빠릅니다. 하지만 최악의 경우에는 이 두 정렬보다 더 느려지는 결과를 가져오기도 합니다.
알고리즘
퀵 정렬의 알고리즘은 다음과 같습니다.
- 리스트의 원소들 중 하나를 pivot으로 정한다.
- pivot을 기준으로 작은 원소들은 왼쪽 큰 원소들은 오른쪽으로 위치시켜 그룹으로 나눈다.
- 1,2의 과정을 원소가 0개 또는 1개가 남을 때까지 진행한다.
힙 정렬 예시
{ 5, 1, 7, 9, 2} 순서대로 원소가 존재한다고 가정했을 때 퀵 정렬의 예시는 다음과 같습니다.
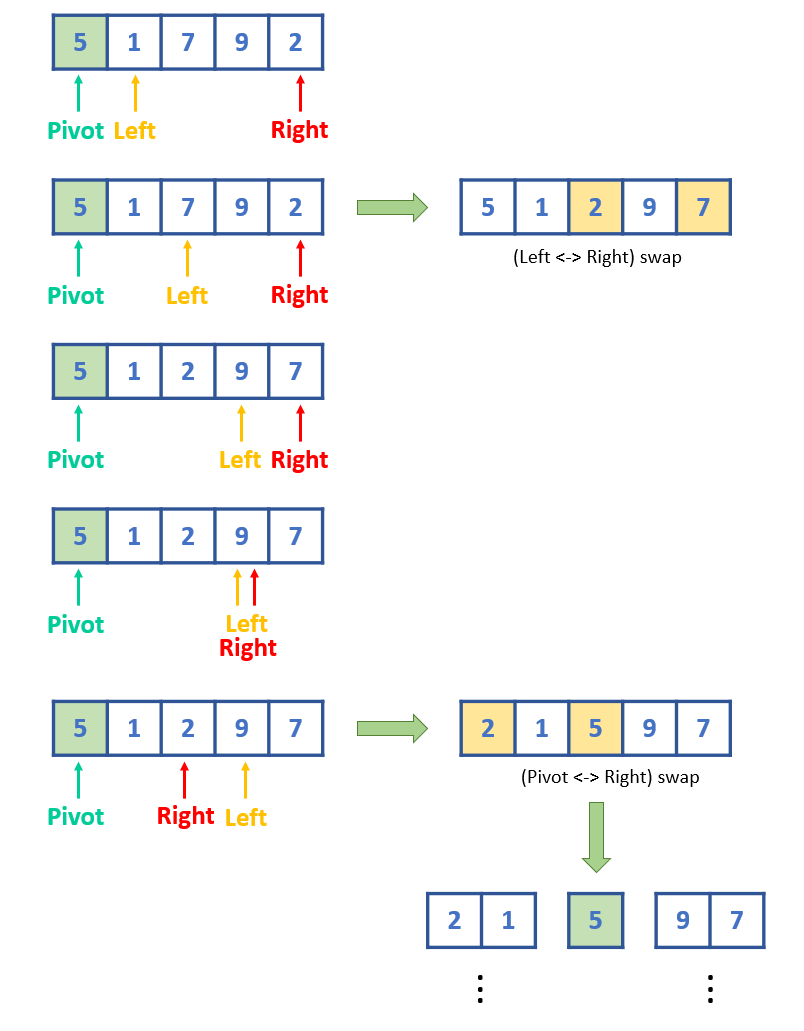
pivot을 정하는 기준은 정해져 있지 않고 가장 앞 원소, 가장 뒷 원소, 무작위 원소 등 여러 가지가 될 수 있습니다. 아래 예시에서는 가장 앞 원소를 pivot으로 정하겠습니다. 그리고 pivot을 기준으로 작은 수, 큰 수를 나누기 위해 left와 right라는 위치 값을 저장하는 변수를 이용합니다.
규칙은 이렇습니다. left 먼저 우측으로 움직이면서 pivot보다 큰 수가 있다면 멈춥니다. 그리고 right가 좌측으로 움직이면서 pivot보다 작은 수가 있다면 멈추고 left와 right의 값을 스왑 합니다. 이 과정을 계속 진행하다가 left와 right의 위치 값이 역전되는 순간, pivot과 right의 값을 스왑하고 종료시킵니다. 그러면 결과는 pivot을 기준으로 작은 숫자들은 좌측에, 큰 숫자들은 우측에 모이게 됩니다. 하지만 작은 숫자들끼리, 큰 숫자들끼리는 정렬되지 않은 상태기 때문에 pivot의 위치는 고정시키고 작은 숫자 그룹, 큰 숫자 그룹을 위와 같은 방법으로 진행합니다. 이렇게 분할된 그룹들의 원소의 개수가 모두 0개 또는 1개가 될 때까지 진행시키면 리스트의 원소들은 모두 정렬됩니다.
시간 복잡도 계산
퀵 정렬의 시간복잡도는 최악, 최상의 경우가 다릅니다.
Pivot을 기준으로 계속해서 두 개의 그룹으로 나눠진다는 점에서 트리의 깊이는 병합 정렬과 같이 \( \log n \)입니다. 그리고 정렬시키는 과정은 left와 right가 매번 한 칸씩 움직이기 때문에 결국 같은 깊이의 정렬 횟수를 모두 합치면 n번이라고 볼 수 있습니다. 그래서 깊이 \( \log n \)을 매번 n번의 비교과정이 필요하기 때문에 결국 시간 복잡도는 \( O(n \log n) \)가 됩니다.
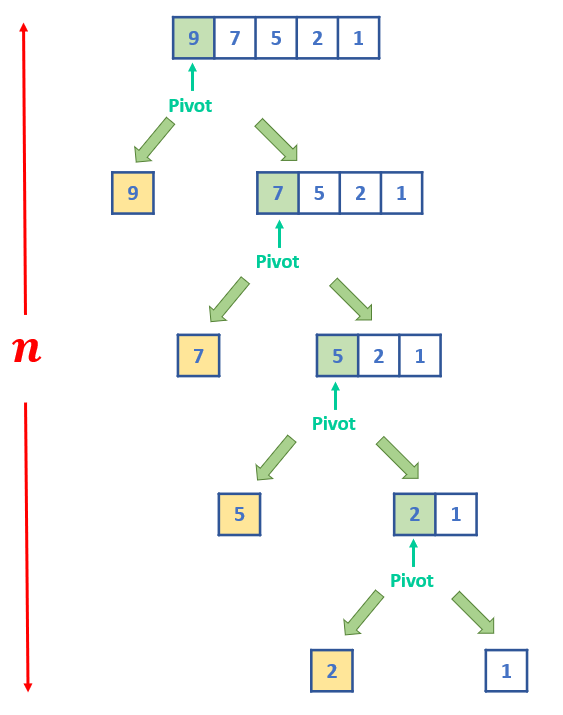
하지만 \( O(n \log n) \)은 퀵 정렬의 평균적인 시간 복잡도입니다. 위에서 말했듯이 최악, 최상의 경우가 다른데 결론부터 말하자면 최악의 경우 \( O(n^2) \)가 되어버립니다. 아래 그림처럼 정렬의 역순으로 배치가 되어있다면, pivot을 기준으로 작은 값이 존재하지 않게 됩니다. 결국 매번 1개의 원소만 줄어들기 때문에 트리의 깊이는 \( n \)입니다. 그래서 마찬가지로 매번 n번의 정렬과정이 필요하기 때문에 시간 복잡도는 \( O(n^2) \)입니다.
C++ Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> arr = {9,1,7,5,2};
void quick_sort(int s, int e){
if( s >= e ) return;
int pivot = s, left = s+1, right = e;
while(left <= right){
while(arr[left] < arr[pivot] && left <= e) left++;
while(arr[right] > arr[pivot] && right > 0) right--;
if(left <= right) swap(arr[left], arr[right]);
else swap(arr[pivot], arr[right]);
}
quick_sort(s, right-1);
quick_sort(right+1, e);
}
int main()
{
quick_sort(0,arr.size()-1);
for(int i=0; i<arr.size(); i++)
cout << arr[i];
}'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Sort #5 - 힙 정렬 Heap Sort (0) | 2021.01.09 |
|---|---|
| [Algorithm] Sort #4 - 병합 정렬 Merge Sort (0) | 2021.01.08 |
| [Algorithm] Sort #3 - 삽입 정렬 Insertion Sort (1) | 2021.01.04 |
| [Algorithm] Sort #2 - 선택 정렬 Selection Sort (0) | 2021.01.02 |
| [Algorithm] Sort #1 - 버블 정렬 Bubble Sort (0) | 2020.12.29 |
![[Algorithm] Sort #6 - 퀵 정렬 Quick Sort](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Frl152%2FbtqTkha2RHO%2FAAAAAAAAAAAAAAAAAAAAAG7mkJB-PVE32jyxCvM8ha3WJw3FZsisHOcS9ovXt6o7%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3D0ORdh3gOGwDusWIalJVRRU4lVWg%253D)