알고리즘 분류
BFS (너비 우선 탐색)
시간 복잡도
\( O(V + E) \)
문제 링크
https://www.acmicpc.net/problem/13549

해당 문제는 대표적인 BFS 문제입니다. 현재 위치 N에서 목적지 K까지 가는데 가장 최소 시간을 구해야 합니다. 이처럼 탐색을 하는 데 있어 최소 시간을 구하는 문제는 DFS보다는 BFS를 이용해야 시간 초과가 나지 않습니다. BFS의 핵심은 "해당 지점에서 갈 수 있는 곳을 다시 Queue에 넣는다" 입니다. 이때 중복되는 지점을 계속해서 탐색을 한다면 시간 초과가 발생하기 때문에 꼭 잘 체크해서 Queue에 넣어줘야 합니다.
BFS 문제는 많이 풀다 보면 비슷한 템플릿이 있다는 것을 알게 됩니다. 템플릿은 보통 아래와 같습니다.
- 입력 변수들 선언 및 초기화
- 가장 처음 지점 Queue에 push 및 방문 시간 체크
- Queue에서 pop한 시점에서 목적지인지 체크
- Queue에서 pop한 지점으로부터 갈 수 있는 다음 지점 push 및 방문 시간 체크
이번 문제에서는 한 지점으로부터 갈 수 있는 후보는 현 위치로부터 +1, -1, x2 위치로 총 3가지입니다. 이때 3가지 중 이미 방문한 곳의 시간보다 큰 경우와 갈 수 있는 범위를 초과한 경우는 제외하고 Queue에 push 후 방문 기록을 체크해줍니다. 3가지 후보를 보통 for문과 if문을 이용해서 각각 체크하게 되는데 이때 주의해야 할 점은 x2로 순간 이동하는 방법은 시간이 0초 증가이므로 if문의 가장 첫 번째에 있어야 합니다. 모든 조건을 만족하고 Queue에 넣을 수 있는 단계가 된다면 push를 해주고 현재 시간을 visit 변수에 체크해줍니다.
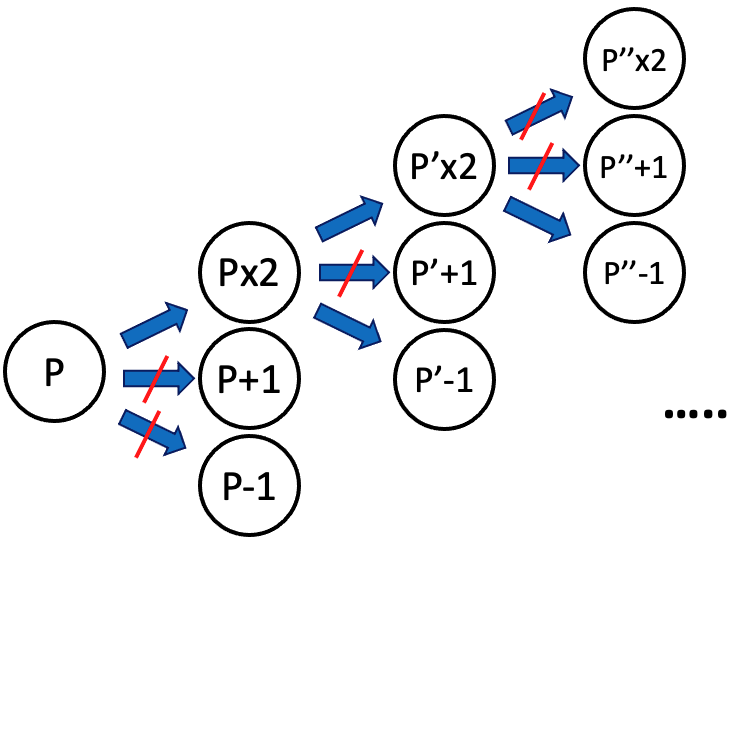
이 문제의 BFS 그림을 그리자면 아래와 같습니다. 가장 처음 위치를 P라고 가정했을 때 P로부터 갈 수 있는 3가지 후보 중 조건에 맞는 위치만 Queue에 넣어줍니다. 그리고 다시 Queue에서 pop한 위치로부터 갈 수 있는 3가지 후보 중 조건에 맞는 위치만 Queue에 넣어줍니다. 이 과정을 원하는 목적지에 도착할 때까지 계속 반복합니다. Queue에서 pop한 시점에 목적지인지 체크하고 목적지라면 그 시간이 최소 시간입니다.
Java
import java.util.*;
public class Main {
public static class Pos{
public int p,d;
Pos(int P, int D){
p = P;
d = D;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
int[] visit = new int[100001];
Queue<Pos> q = new LinkedList<Pos>();
int ans = 0;
Arrays.fill(visit,987654321);
q.add(new Pos(n,0));
visit[n] = 0;
while(!q.isEmpty()){
Pos cur = q.poll();
if(cur.p == k){
ans = cur.d;
break;
}
for(int i=0, nextP, nextD; i<3; i++){
if(i==0) {
nextP = cur.p * 2;
nextD = cur.d;
}
else if(i==1) {
nextP = cur.p - 1;
nextD = cur.d + 1;
}
else {
nextP = cur.p + 1;
nextD = cur.d + 1;
}
if(nextP < 0 || nextP >= 100001) continue;
if(visit[nextP] < nextD) continue;
visit[nextP] = nextD;
q.add(new Pos(nextP, nextD));
}
}
System.out.println(ans);
}
}'Algorithm 문제 풀이 > 백준' 카테고리의 다른 글
| [Algorithm][Union Find] 백준 1717 - 집합의 표현 (0) | 2021.10.08 |
|---|---|
| [Algorithm][투 포인터] 백준 1806 - 부분합 (0) | 2021.10.06 |
| [Algorithm][부분 합] 백준 11659 - 구간 합 구하기 4 (0) | 2021.09.29 |
| [Algorithm][위상 정렬] 백준 2252 - 줄 세우기 (0) | 2021.09.28 |
![[Algorithm][BFS] 백준 13549 - 숨바꼭질 3](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Ft30I4%2FbtrgD3AsbES%2FAAAAAAAAAAAAAAAAAAAAAK0HmEtV_9UiprnJMiydnd0_mOBmIOmgR4WoktreB5Ed%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DCfDdT803guUuMVTDb8wsT%252B7YqKg%253D)