알고리즘 분류
Union Find
시간 복잡도
\( O(N) \)
문제 링크
https://www.acmicpc.net/problem/1717

이번 문제의 알고리즘 종류는 Union Find입니다. 많은 수가 있을 때 특정 수들이 같은 집합인가?라는 물음에 대해 효율적으로 사용할 수 있는 알고리즘입니다. Union Find의 핵심은 "같은 집합이면 같은 루트"입니다. 처음에는 모든 수들이 자기 자신을 루트로 가지고 있도록 초기화를 시켜놓습니다. 하지만 두 수를 merge 한다면 각 수의 루트 값들이 부모, 자식의 관계를 가지게 됩니다. ( 아래 예시를 보면 이해가 가능합니다. ) 그리고 서로 같은 집합임을 알고싶다면 각 숫자들의 최상단 부모, 즉 루트 값을 비교할 수 있습니다.
하지만 이렇게 계속 진행하다보면 1 -> 2 -> 3 -> 4 -> 5 -> 6 이런 식으로 줄지어서 부모를 가지게 되는 최악의 경우의 수가 있습니다. 이런 경우 1이라는 숫자는 최상단 루트의 값을 알기 위해서는 총 \( N-1 \)번의 연산이 필요합니다. 그러면 결국 \( N \)개 수의 대해서 최악의 경우 시간 복잡도는 \( O(N^2) \)를 가지게 되므로 N이 10만 이상이라면 시간 초과가 발생할 것입니다.
그래서 위에서 핵심을 말했듯이 서로 같은 집합에 속해있다면 각 수들은 루트만 기억하도록 하는 것입니다. 그러면 모든 수는 자신의 루트를 찾는데 \( O(1) \)의 시간이 걸리게 함으로써 더욱 빠른 시간복잡도를 가지게 됩니다. 참고로 최상단 부모, 즉 루트 값은 find 함수가 호출되는 시점에 업데이트가 됩니다.
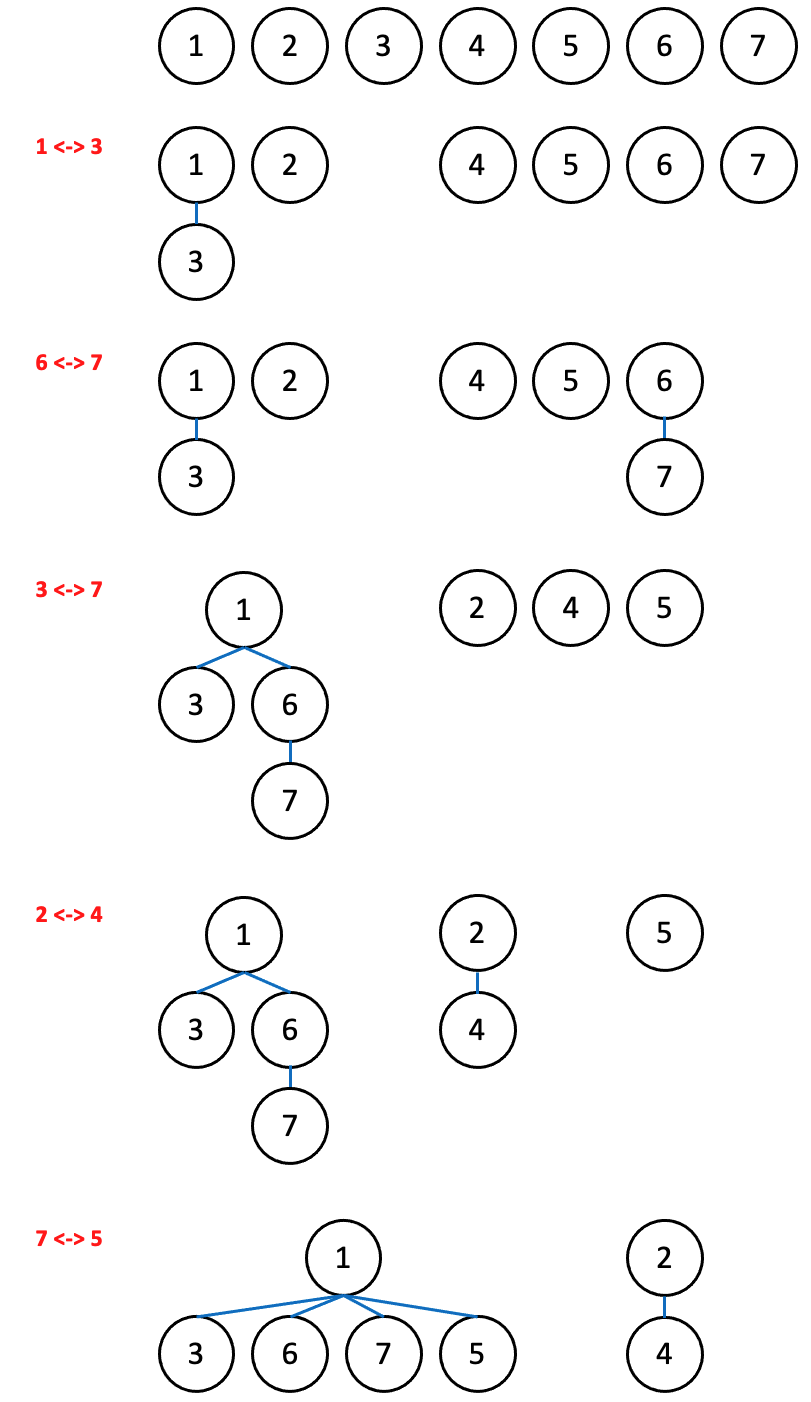
이번 문제는 Union Find의 가장 기본적인 문제입니다. Union Find의 문제는 merge와 find만 구현하면 거의 다 해결했다고 볼 수 있습니다. 아래의 예시는 1 ~ 7의 숫자들이 여러 과정의 merge가 이루어지는 결과를 보여줍니다. ( 마지막 예시인 7과 5가 merge 될 때 7은 이 시점에서 루트 값을 업데이트합니다. )
Java
import java.util.*;
public class Main {
static int[] p = new int[1000001];
public static int find(int n){
if(p[n] == n) return n;
return p[n] = find(p[n]);
}
public static void merge(int a, int b){
a = find(a);
b = find(b);
if(a==b) return;
p[b] = a;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for(int i=1; i<=n; i++)
p[i] = i;
for(int i=0, t,a,b; i<m; i++){
t = sc.nextInt();
a = sc.nextInt();
b = sc.nextInt();
if(t == 0) merge(a,b);
else if(t==1) System.out.println((find(a)==find(b)) ? "YES" : "NO");
}
}
}'Algorithm 문제 풀이 > 백준' 카테고리의 다른 글
| [Algorithm][투 포인터] 백준 1806 - 부분합 (0) | 2021.10.06 |
|---|---|
| [Algorithm][BFS] 백준 13549 - 숨바꼭질 3 (0) | 2021.10.04 |
| [Algorithm][부분 합] 백준 11659 - 구간 합 구하기 4 (0) | 2021.09.29 |
| [Algorithm][위상 정렬] 백준 2252 - 줄 세우기 (0) | 2021.09.28 |
![[Algorithm][Union Find] 백준 1717 - 집합의 표현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbEdFHx%2Fbtrg8EmuM15%2FAAAAAAAAAAAAAAAAAAAAAGbQcj0T-h7I-uOAmOckywFZhxu9Sncen13g-7_m4rLU%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DuDLnsjnwerGBjLvgBMQxKVflVIA%253D)